Ilutaju on teadusliku maailmakäsituse oluline instrument.
Nagu õpilaste teaduslikus ühingus tavaks, on igal aastal Viitnal toimuval suveseminaril oma „kõikeläbiv” teema, mida ühel või teisel määral, ühe või teise vaatenurga piires käsitlevad eri (teadus)valdkondade esindajad. Kusjuures valdkonnad on valitud võimaluse piires nii, et need kataksid mingil määral (vähemalt n-ö naabrussegi sattudes) olulised teadusega seotud alad ja oleksid seejuures ise kaetud võimalike esinejatega. Laias plaanis on mitte väga rangelt mõeldud märksõnadega kirjeldatav jaotus selline: reaal- ja inseneriteadused, eluteadused, teadused inimesest, teadused ühiskonnast, teadused kõiksusest. Veidi detailsemas plaanis jaotub see omakorda matemaatika- (sh informaatika-), füüsika-, keemia-, insenerialadeks; teadusteks taime- ja loomariigist; teadusteks inimese (aju) ehitusest ja toimimisest; teadusteks inimkooslustest; teadusteks kõige vägevamast: universumist, filosoofiast ja usust.
Loomulikult pole mõnepäevasel üritusel võimalik kõiki neid valdkondi valgustada. Kõnelemata sellest, mis nimetamata jäi. Sellesuvisel seminaril oli valdkondade (ning esinejate) nimistu järgmine: matemaatika (Peeter Lorents), füüsika (Enn Saar), keemia (Toomas Kaevand), inseneriala (Toomas Peek), bioloogia (Raik-Hiio Mikelsaar), zooloogia (Aleksei Turovski), neuropsühhofarmakoloogia (Jaanus Harro), semiootika (Mihhail Lotman), filosoofilised ja teoloogilised aspektid (Enn Kasak, Toomas Paul). Pluss korralduse külg: ETAg-i tublid inimesed, keda juhtis Terje Tuisk.
Ilust teaduses
Nõnda võiks üldises plaanis iseloomustada seda, mis suveseminaril 09.–11.08 kõneks tuli. Alustuseks on paslik lähtuda kunagise astrofüüsiku ja nüüd pigem filosoofi Enn Kasaku ettekandes esinenud mõtetest, mida võiks üldistada järgmiseks printsiibiks: ilutaju on teadusliku maailmakäsituse üks olulisimaid instrumente.
Tavaliselt on õige ehk paikapidav ühtaegu ka ilus. Vastupidi ei pruugi alati olla. Tõepoolest – maailma asjade matemaatilist (või mõnele muule teadusele tuginevat) käsitlust luues on mõnigi kord ilust lähtumine andnud käsitletavast vale pildi. Näitena sobib siinkohal hellenistliku ilukäsituse rakendamine taevaste asjade selgitamisel. Antiikses Kreekas domineerinud arusaama kohaselt, mida seostatakse ka Platoni õpetustega, oli taevaliku ilu üks väljendus sfäär (ruumis) ja ring (tasandil). Õppinud taevakehade asendeid ja liikumisi jälgima ning sellekohaseid arvutusi ja jooniseid tegema, kiputi kiretute vaatluste ning andmetöötluse tulemusi „kooskõlastama” üldiseima arusaamaga sellest, mis on ilus. Arusaadavalt asuvad taevakehad taevas ning peavad seega paiknema ja kulgema kooskõlas taevase ilu ja harmooniaga. Taevastel sfääridel pidid asjad liikuma ilusasti: mööda ringjooni. Üha täpsemad vaatlused kippusid aga ikka täpsemini näitama, et planeetide trajektoorideks ei saa olla ringjooned. Ilmavaateliste aluste päästmiseks leiti väljapääs: taevakehad liiguvad kõigest hoolimata mööda ringjoont, aga selle ringjoone keskpunkt peab ka ise liikuma – mingil teisel ringjoonel. Veelgi täpsemad vaatlused nõudsid tulemuste ning ilmavaate kooskõlastamiseks ka kolmandat ringjoont, mille keskpunkt pidanuks liikuma eelmainitud teisel ringjoonel. Jne.
Ringjoonest küünte ja hammastega kinni hoidmine andis küll kooskõla usuga sellesse, mis peab olema ja saab olla ilus, kuid paraku muutis arvutused ning joonised arutult keerukaks. See muutus muuhulgas tülikaks meremeestele, kelle töö (ja sageli ka elu) olenes võimalikult täpsest asukoha määramisest, mida tehti taevakehade asendite mõõtmisest lähtudes. Ringjoontele tuginev süsteem, mille „põhiline keskpunkt” oli Maa ja mida tunti valdavalt Ptolemaiose süsteemina, püsis aga visalt, kuni alles aastal 1605 leidis saksa õpetlane Johannes Kepler pärast aastakümneid kestnud astronoomiliste andmete analüüse ja mõtisklusi, et planeetide orbiitideks pole mitte ringjooned, vaid ellipsid. Mõtlemapanevaks näiteks ilu ja ilmaelu „pealesunnitud” kooskõlastamise kohta on seoses eelesitatuga Robert R. Newtoni 1978. aastal ilmunud raamatus „The Crime of Claudius Ptolemy” toodud argumendid, millele tuginedes võib väita, et Ptolemaios „kohendas” vaatlusandmeid nõnda, et need oleksid kooskõlas „taevaliku ilu” nõuetega …
Süsteemide ilu
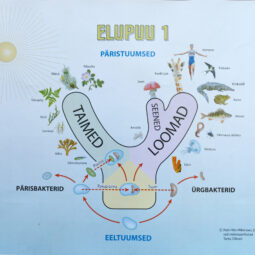
Mitmes ettekandes, mida Viitnal oli võimalik nautida, kõlas mõte ilust, mille toovad esile eri valdkondades loodud süsteemid. Nii on Mendelejevi loodud keemiliste elementide süsteem kahtlemata kaunim kui enne seda keemiat koormanud ainete süsteemi puudumine. Tõsi, ka Mendelejevi süsteemil on omad iluvead, mida on mitmel korral püütud parandada. Üks parendus on seejuures ka eesti õpetlase R. Mikelsaare loodud keemiliste elementide tabel. Temalt pärineb veel üks süsteem: elupuu ehk nn puukujuline süsteem elusolendite ja nende kogumite struktureerimiseks. Elu süsteemides avalduv ilu võib väljenduda nii väljanägemises kui ka käitumises. Mitte ainult looduses olevat ja toimuvat jälgivale inimesele, vaid ka elusolendeile endile, nagu selgitas Aleksei Turovski.
Ilu avaldub ka laitmatult toimivates ning otstarbekalt loodud tehnilistes süsteemides. Olgu selleks siis enam kui sajandivanune seadeldis kelladetailide treimiseks või hoopis mõni tänapäevane sidesüsteem. Tõeline insener loob ilu ja mõistab seda. See tunne tekkis Toomas Peegi ettekannet kuulates. Olgu öeldud, et insener Peek püsis tema mõtetest innustunud õpilasteadurite intellektuaalses piiramisrõngas kella kolmeni öösel.
Tehniliste süsteemide ülesehitus ja toimimine peab olema kooskõlas füüsikast tuntud tõsiasjadega, sh valemitega, mis olemuselt pole ju muud kui teatavad sümbolite süsteemid. Osa valemeid (ja nendega seotud teooriaid) peetakse vägagi ilusaiks (nt kuulsad Einsteini valemid), kõnelemata nähtustest, mida nende abil selgitatakse. On see siis maailmaruumi ehitus või selles toimuvad ülivõimsad, lausa katastroofi olemusega nähtused, nagu näiteks galaktikate kokkupõrked. Kuid ka sedalaadi üliõudused võivad omal moel ilusad olla, nagu nähtus Enn Saare ettekandest. Süsteemide ilu võib avalduda selleski, kuidas üks või teine keemiline aine on üles ehitatud või milliseid teisi aineid selleks lagundama või ühendama peab.
Vahel lisandub selliste reaktsioonide ilule midagi säärast, mida võib kirjeldada sõnaga elegantsus. Asjakohaseid näiteid ja selgitusi võis näha/kuulda keemik Toomas Kaevandi ettekandes.
Ootamatuse ilu
Toomas Kaevand esitas omapärase näite sellest, kuidas Esimese maailmasõja aegsed liitlased arvutasid välja, millal peaks keiserliku Saksamaa relvadest kõlama viimased lasud, kuna … laskemoona koosseisus olevad lämmastikuühendid (mida Saksamaal enda loodusvarade hulgas polnud) pidid lihtsalt otsa lõppema. Paraku paukusid sakslaste püssid veel aastaid edasi, sest leiti tõeliselt nutikas, võiks öelda lausa elegantne viis vajalike ainete sünteesiks.
Sedalaadi ilu, mis avaldub sageli ootamatuses, ilmneb ka matemaatikas. Selle olemus on tihti seotud nn lõikereegli rakendamisega. Lühidalt seisneb asi järgmises: mõnel juhul on pea võimatu veenda ja veenduda, et ühest asjast, ütleme A-st, tuleneb teine asi, ütleme B. Samas aga, nagu mõnele õnnelikule õpetlasele lõpuks selgub, on täiesti võimalik jõuda A-st hoopis asjani C. C-st aga omakorda asjani B. Seega ongi näidatud, et A-st ikkagi tuleneb B! Lõikereegliga seotud probleeme uuris oma doktoritöös saksa matemaatik Gerhard Gentzen. Töö tulemused avaldati aastal 1934. Neist selgus, et teatavate loogiliste süsteemide korral on „elegantsetest ootamatustest” ehk siis lõikereegli rakendustest võimalik lahti saada (kui kasutada Gentzeni pakutud reduktsioone). Paraku on sellel oma hind: lõiketa (ehk „elegantsete vahetulemusteta”) tõestused võivad osutuda tunduvalt mahukamateks ja keerukamateks.
Ilu ja selgus
Matemaatikud, nagu paljude teistegi teaduste ning insenerialade esindajad, on täheldanud, et iluga seostub valdavalt selgus. Ühest küljest avaldub see eespool juba nimetatud süsteemsuses (ehk selles, et on fikseeritav, mis on need asjad – objektid, nähtused vms –, millega me tegeleme ning lisaks on fikseeritavad nende asjade oluliseks peetavad omadused või asjadevahelised seosed). Kui sedalaadi fikseeritavust pole, pole ka selgust. Ja ühtlasi pole paljude jaoks ilu. Selgusel võib aga olla teinegi tahk: figureerimine tähiseks-tähenduseks olemise seoses. See seos on olemuselt fundamentaalseos, nagu näiteks hulkadevaheline ehk ühe hulga teise elemendiks olemise seos. Fundamentaalseosed ei kuulu määratlemisele. Nende olemuse mõistmisel lähtutakse asjakohastest (tõestamisele mittekuuluvatest) põhipostulaatidest. Nii postuleeritakse elemendiks olemise kohta, et leidub säärane hulk, mille elemendiks ei olda. Tähiseks/tähenduseks olemise kohta postuleeritakse aga näiteks, et asjadel võib olla mitmeid tähiseid ja ka mitmeid tähendusi. Sõnadesse „võib olla” tuleb seejuures suhtuda tõsiselt. „Võib olla” pole sama mis „peab olema” ega ka sama mis „ei saa olla”. Nii nagu iga hulga elemendiks ei olda, pole iga asi ka ilmtingimata millelegi tähis või tähendus. Selguse jaoks on tähiste ja tähenduste olemasolu aga vajalik. Kusjuures, nagu juba öeldud: pole selgust, pole ka ilu. Paljude jaoks. Paljude jaoks aga pole sugugi sama, mis enamiku või lausa kõikide jaoks!
Küllap on neidki, kellele ilu seostub seletamatuse, saladuslikkuse ja muu sarnasega. Sellele asjaolule juhtis tähelepanu Toomas Paul, esitades iluga seotud iidseid rahvatarkusi. Tähenduste seos iluga seostub omakorda semiootika uurimisvaldkondadega, mida käsitles Mihhail Lotman. Sealhulgas illustreeris ta osa oma esitusest veenvate näidetega silmale nähtavast ilust nii tänapäevaste kui ka kunagise Iraani šahhi ettekujutuste kohaselt (püüdke silme ette manada pehmelt öeldes tüsedapoolset idamaist keskealist emandat napivõitu baleriinikostüümis, mida kõike olevat pildistanud auline šahh ise, kuna oma mehe naist ei tohtinud teine meeshing, sh fotograaf, näha; küll aga tohtis võõras mees vaadata pilti).
Ilu ning ajutegevus, logaritmid veel sealjuures
Suur osa sellest, mis ilusana ilmneb, kulgeb inimese jaoks aju ning selle tegevuse kaudu. Ajul on oma ülesehitus, koostisosad (nt ajupiirkonnad, neuronid ja nendevahelised ühendused). Väga keerulise aparatuuri (nt teatavat tüüpi tomograafid) abil on võimalik jälgida ajutegevuse aktiivsuse ilminguid näiteks siis, kui inimesed hindavad ühe või teise valemi ilu. Seejuures toimuvad ajus elektromagnetiliste kaasnähtustega biokeemilised protsessid, mida võivad mõjutada mitmesugused ained, näiteks ravimid või, vastupidi, mürgid (nt paljud narkootikumid). Nimetatud ainete olemasolu, kuid ka kogus võib seostuda seisundiga, kus inimene on kestvalt ja sügavalt rusutud ega ole suuteline midagi ilusana nägema. Või siis vastupidi – kõik on nii kaunis, et mine või lolliks (et mitte öelda oledki juba lolliks läinud). Neid asju uurib neuropsühhofarmakoloogia, millega seotud aspekte valgustas oma ettekandes Jaanus Harro. Temagi ei pääsenud 90 minutiga, vaid pidi veel tundide kaupa vahetpidamata ja püstijalu õpilasteadurite küsimustele vastama.
Inimaju ülesehitus ja selle toimimine on teatavatel põhjustel allutatud seaduspärasustele, mida on täheldanud mitmed uurijad, sh saksa õpetlased Ernst Heinrich Weber (1795–1878, eksperimentaalpsühholoogia üks rajajatest) ning Gustav Theodor Fechner (1801–1887, psühhofüüsika üks rajajatest), samuti Ameerika psühholoog, Harvardi psühhoakustika labori rajaja Stanley Smith Stevens (1906–1973). Üks nende õpetlaste sõnastatud seaduste „üldsõnastus” võiks kõlada järgmiselt: kui ärrituse tajumine (nt mingi undamine) on hinnatav arvuliselt ja seda ärritust esile kutsuv ärritaja (pisut lärmakalt töötav ventilaator) on iseloomustatav arvuliselt, on ärrituse tajumisega seotud arv ning ärritaja toimimisega seotud arv (nt ventilaatori pöörete arv sekundis) omavahel logaritmilises sõltuvuses. Nii oleneb tänapäevase klaveri mingi klahvi vajutamisel tekkiva heli tajutav kõrgus (st kas selle või järgmise või hoopis ülejärgmise vms klahviga seotud heli) logaritmiliselt kõlava heli sagedusest. Midagi sarnast ilmneb rütmide ja tempo ning palju muu tajumisel.
Kusjuures paljude jaoks on selge logaritmiline seos selleks, mille alusel asjad ilusad tunduvad. Kuid mitte alati! On palju neidki, kelle jaoks helide ilu ei seostu logaritmilise olenevusega ja kelle jaoks on ilu aluseks hoopis nn naturaalne häälestus.
Ilu ja pillid, pillid ja pillerkaar – kaugetel aegadel oli sedalaadi asjade vahel otsene side: ilu = ilo. Sellele (et muuhulgas pill tuleb pika ilu peale) juhtis tähelepanu ka Toomas Paul, kelle ettekanne andis ilule teataval määral usulise vaate. Teadusele pole seegi liigne, sest tahame või mitte – paljude (täppis)teaduste, sh matemaatika, füüsika, keemia, bioloogia jt alused pole olemuselt muud kui uskumiseks antud tõed. Nii lihtsalt on. Sarnaselt iluga ehk täpsemalt sellega, mida aegade ja kohtade, kokkulepete ning uskumuste raames on just tähenduse ja ülesehituse poolest ilusaks loetud.
Mis aga on järgmise, kaheteistkümnenda ÕTÜ suveseminari peateema? See on esialgu üks ilus saladus, mis laheneb kevadel ÕTÜ teadusfestivali viimasel päeval.






Lisa kommentaar